Abbiamo già accennato, in precedenza, che le carte altro non sono che delle proiezioni della superficie terrestre. Ora vediamo di che tipo sono.
Le proiezioni azimutali, cioè su un piano, si classificano in polari, equatoriali o oblique a seconda che il piano sia tangente all’ellissoide rispettivamente ad un polo, ad un punto dell’equatore o un qualsiasi altro punto della superficie.
In base poi alla posizione della sorgente dei raggi proiettanti si distinguono in gnomoniche (sorgente al centro dell’ellissoide), stereografiche (sorgente agli antipodi del punto di tangenza), ortografiche (sorgente all’infinito, raggi proiettanti paralleli).

Le proiezioni cilindriche, in base all’orientamento del cilindro si definiscono in proiezioni dirette, inverse o trasverse e oblique.
Nella proiezione diretta tangente il cilindro è tangente all’equatore, se secante il cilindro interseca l’ellissoide in due paralleli.
Nella proiezione cilindrica inversa tangente, il cilindro è tangente lungo un meridiano, mentre nelle proiezioni cilindriche inverse secanti, il cilindro ha diametro inferiore.

Modifiche geometriche nella posizione della sorgente dei raggi proiettanti o squisitamente analitiche possono conferire caratteristiche geometriche diverse anche a tali carte.
Una proiezione cilindrica inversa a cilindro secante molto importante è la proiezione di Gauss, su cui si basano tra gli altri i sistemi UTM, Gauss-Boaga e Gauss-Kruger (ne riparleremo in seguito).
Nelle proiezioni coniche, il cono di proiezione può essere tangente o secante il globo.
Nel primo caso le due superfici si toccano lungo un meridiano, detto meridiano standard, nel secondo le superfici si intersecano in due meridiani, che prendono ugualmente il nome di meridiani standard.
In entrambi i casi i meridiani sono proiettati sulla superficie conica incontrandosi al vertice del cono.
I paralleli si presentano come archi di circonferenza, mentre i meridiani sono delle rette convergenti.
Il cono per essere svolto e tagliato poi lungo un meridiano, il cui antimeridiano risulta poi essere il meridiano centrale della proiezione.

Carte e sistemi di proiezione
Rispetto alle loro proprietà prevalenti, le proiezioni si distinguono in equidistanti, equivalenti e conformi, a seconda che mantengano inalterate le distanze, le aree o gli angoli. Al variare dei principi usati per la loro realizzazione, le proiezioni si dividono in vere e convenzionali. Le vere si basano su principi geometrici e matematici. Le convenzionali, seppure derivate dalle vere, utilizzano espedienti che minimizzano le deformazioni o permettono di giungere a risultati prefissati.
Ora analizzeremo in maniera più chiara tre proiezioni.
Proiezioni Prospettiche, ottenute mediante un piano tangente alla sfera in un punto qualunque della stessa. Vista la zona ristretta rappresentata, l’errore della deformazione è irrilevante.
Si realizzano, per esempio, gli stradari delle città o dei paesi.
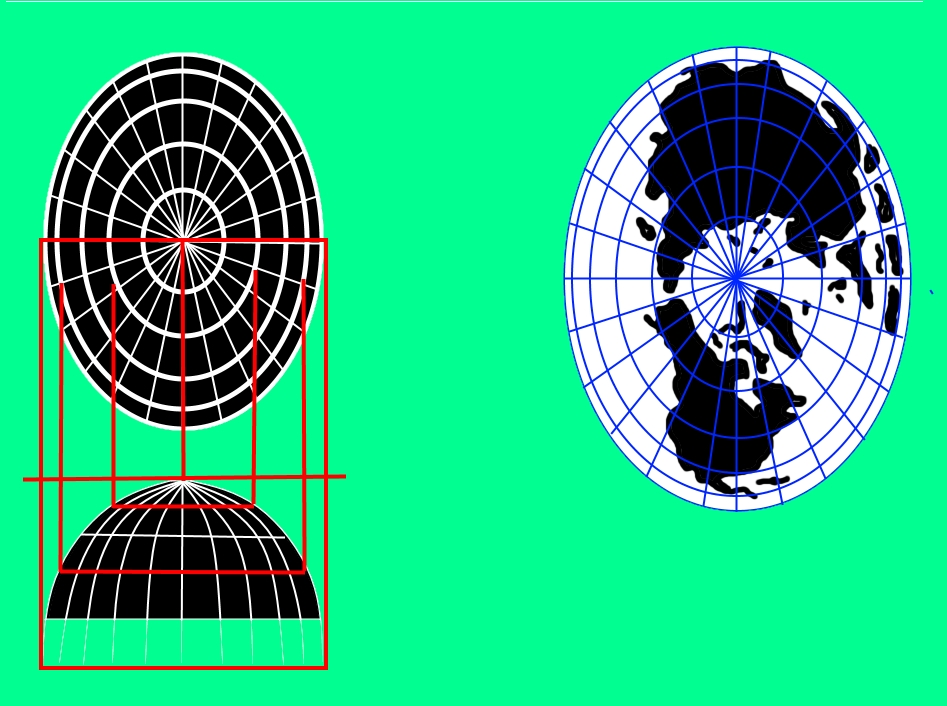
Proiezione di Lambert: Sono proiezioni coniche, si realizzano proiettando i punti della sfera su un cono tangente ad un parallelo. Le deformazioni vengono compensate con apposite formule matematiche.

Proiezione di Mercatore: Proiezioni cilindriche, si ottengono avvolgendo il globo con un cilindro tangente all’Equatore. Le deformazioni vengono compensate con apposite formule matematiche.

Particolarità della carte Mercatore e Lambert
La proiezione isogona di Mercatore è una cilindrica modificata in cui i meridiani rimangono equidistanti, mentre i paralleli, spostandosi dall’Equatore ai Poli, si allontanano reciprocamente in proporzione a quanto la distanza dei meridiani è maggiorata sulla carta rispetto alla realtà. Questa proiezione rende la carta conforme, mentre le superfici si deformano sempre più con l’avvicinarsi ai Poli (ad esempio la Groenlandia appare più vasta dell’America Meridionale).
Da notare che i meridiani mantengono sempre lo stesso angolo con i paralleli, tagliandoli sempre a 90°, pur se non conforme alla realtà.
Nella azimutale equivalente di Lambert, che ha il punto di osservazione all’infinito, i meridiani sono rettilinei e perpendicolari all’Equatore e si avvicinano, fra loro, avvicinandosi ai poli, i paralleli, invece, si infittiscono a mano a mano che si avvicinano al Polo, il quale risulta essere un segmento e non un punto.
Da notare che i meridiani tagliano ogni parallelo attraversato, con angolazione differente. Ogni meridiano, taglia lo stesso parallelo con lo stesso angolo.
Proiezione di Gauss
E’ la proiezione su cui si basa il sistema UTM (Universo Traverso Mercatore) che si sta imponendo come lo standard cartografico a livello mondiale, ed il sistema nazionale italiano Gauss-Boaga.
Si può considerare derivata da una proiezione cilindrica inversa secante, ma con trasformazione analitica e non geometrica
La corrispondenza biunivoca tra i punti dell’ellissoide e quelli del piano fu stabilita da Gauss nel 1820 affinchè fossero verificate le seguenti condizioni:
- ottenere una carta conforme
- che le immagini del meridiano centrale e dell’equatore fossero rette
- che la rappresentazione fosse equidistante sul meridiano centrale.
La rappresentazione, essendo puramente analitica, è detta più propriamente proiezione conforme analitica inversa di Gauss, o anche “proiezione trasversa di Mercatore”.
Alla carta si suole aggiungere un reticolo chilometrico (di coordinate cartesiane), che a causa delle deformazioni dei meridiani e dei paralleli si presentano corrispondenti solo il meridiano centrale con la linea X = 0 e l’equatore con la linea Y = 0 (sono gli assi del sistema di riferimento cartesiano). Ciò ha un’implicazione nella definizione di Nord
Affinchè le deformazioni siano contenute in una tolleranza assegnata (quella compatibile con la scala) la parte di ellissoide rappresentata è limitata ad un fuso di piccola ampiezza, 6° nel sistema UTM.
Il cilindro secante permette di ridurre le deformazioni rispetto al cilindro tangente.
Dal punto di vista analitico si è introdotto un fattore di riduzione, attualmente in uso sia nel sistema Gauss-Boaga, sia nel sistema UTM.
Un’ultima proprietà notevole è che all’interno del fuso la linea più breve congiungente due punti (geodetica) è rappresentata da una curva a curvatura leggerissima, detta trasformata, che ha quindi lunghezza praticamente pari alla sua corda.
